矩阵

由 m * n 个数排成的 m 行 n 列的数表称为m行n列的矩阵，简称 m*n 矩阵

以下是一个 2*3 矩阵

\begin{array}{r} (\begin{array}{c} 1 & 3 & 6 \\ 4 & 6 & 9 \end{array}) \end{array}

基本运算

只有同型矩阵之间才能进行加减法运算

\begin{array}{r} (\begin{array}{c} a_{11} & a_{12} & . . . & a_{1 n} \\ a_{21} & a_{22} & . . . & a_{2 n} \end{array}) + (\begin{array}{c} b_{11} & b_{12} & . . . & b_{1 n} \\ b_{21} & b_{22} & . . . & b_{2 n} \end{array}) \\ = (\begin{array}{c} a_{11} + b_{11} & a_{12} + b_{12} & . . . & a_{1 n} + b_{1 n} \\ a_{21} + b_{21} & a_{22} + b_{22} & . . . & a_{2 n} + b_{2 n} \end{array}) \end{array}

运算律：
交换律： A + B = B + A
结合律： (A + B) + C = A + (B + C)

把矩阵 A 的行和列互相交换所产生的矩阵称为A的转置矩阵

\begin{array}{r} {(\begin{array}{c} 1 & 3 & 6 \\ 4 & 6 & 9 \end{array})}^{T} = (\begin{array}{c} 1 & 4 \\ 3 & 6 \\ 6 & 9 \end{array}) \end{array}

运算律：
$(A B)^{T} = B^{T} A^{T}$

\begin{array}{r} (M \times N) (N \times P) = (M \times P) \\ (\begin{array}{c} 1 & 3 \\ 4 & 6 \\ 0 & 4 \end{array}) (\begin{array}{c} 3 & 6 & 9 & 4 \\ 2 & 7 & 8 & 3 \end{array}) \end{array}

结果中 m*n 的数，是由 A 的 m 行和 B 的 n 列相乘得出来

2D 点 = (x, y, 1)ᵀ

2D 向量 = (x, y, 0)ᵀ

这样定义满足以下实现
vector + vector = vector
point - point = vector
point + vector = point （点沿着一个向量移动一定距离，最后还是点）

旋转、缩放都是线性变换，比如在二维上可以用一个 2*2 矩阵完成

\begin{array}{r} (\begin{array}{c} a & b \\ c & d \end{array}) \end{array}

但是平移不是线性变换，不能用一个 2*2 矩阵乘一个二维向量实现

这个时候引入一个齐次坐标，把矩阵增加一个维度，就可以实现平移

\begin{array}{r} (\begin{array}{c} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{array}) \times (\begin{array}{c} x \\ y \\ 0 \end{array}) = (\begin{array}{c} x + t_{x} \\ y + t_{y} \\ 0 \end{array}) \end{array}

至此，旋转、缩放、平移都可以通过增加一个齐次坐标，形成 3*3 矩阵，完成矩阵模型

S (s_{x}, s_{y}) = (\begin{matrix} s_{x} & 0 & 0 \\ 0 & s_{y} & 0 \\ 0 & 0 & 1 \end{matrix})

以原点为中心进行逆时针旋转

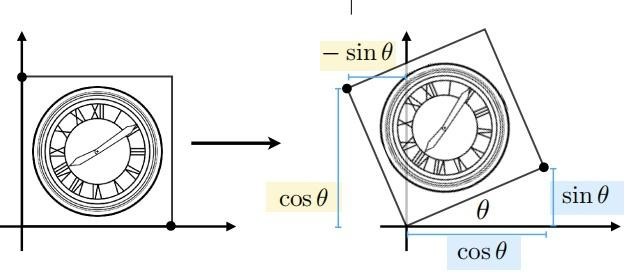
R (α) = (\begin{matrix} c o s α & - s i n α & 0 \\ s i n α & c o s α & 0 \\ 0 & 0 & 1 \end{matrix})

顺时针旋转为上面矩阵的逆矩阵

\begin{array}{r} R (- α) = (\begin{array}{c} c o s α & s i n α & 0 \\ - s i n α & c o s α & 0 \\ 0 & 0 & 1 \end{array}) = R (α)^{T} \end{array}

T (t_{x}, t_{y}) = (\begin{matrix} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{matrix})

矩阵需要经历一系列变换 A1, A2, ..., An

先生效的变换，应该先作用，所以在公式上从右到左的

A_{n} . . . A_{2} A_{1} (\begin{matrix} x \\ y \\ 1 \end{matrix})

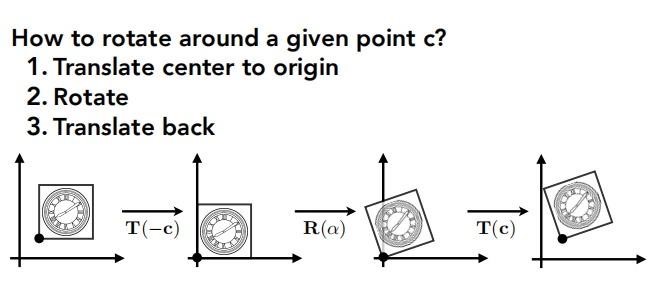
如何绕某一个点旋转
先把那个点平移到原点，然后进行旋转，最后再反向平移回去
$T (c) R (α) T (- c)$

绕 X、Y、Z 轴旋转

\begin{array}{r} R_{X} (α) = (\begin{array}{c} 1 & 0 & 0 & 0 \\ 0 & c o s α & - s i n α & 0 \\ 0 & s i n α & c o s α & 0 \\ 0 & 0 & 0 & 1 \end{array}) \\ R_{y} (α) = (\begin{array}{c} c o s α & 0 & s i n α & 0 \\ 0 & 1 & 0 & 0 \\ - s i n α & 0 & c o s α & 0 \\ 0 & 0 & 0 & 1 \end{array}) \\ R_{z} (α) = (\begin{array}{c} c o s α & - s i n α & 0 & 0 \\ s i n α & c o s α & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}) \end{array}

理解：
为什么绕 X 轴旋转，矩阵 1x1 的位置为 1
因为绕 X 轴旋转，则 x 位置不变，所以为1，其余位置坐旋转
为什么绕 Y 轴旋转，是逆矩阵
因为Y轴是，Z叉乘X得到的，所以是相反的