向量

定义

向量是一种同时具有大小和方向的物理量

同时具有大小和方向的物理量称为向量值物理量。常见的向量值物理量有：力（在某个特定方向上施加一定的作用力——量值），位移（在某个净方向上移动一段距离），速度（速率和方向）。因此，向量可以用来表示力、位移和速度。有时我们也用向量来表示一个单个方向。

在数学上，写法是把向量的起点终点写在一起，再用箭头相连，注意起点在前，终点在后。

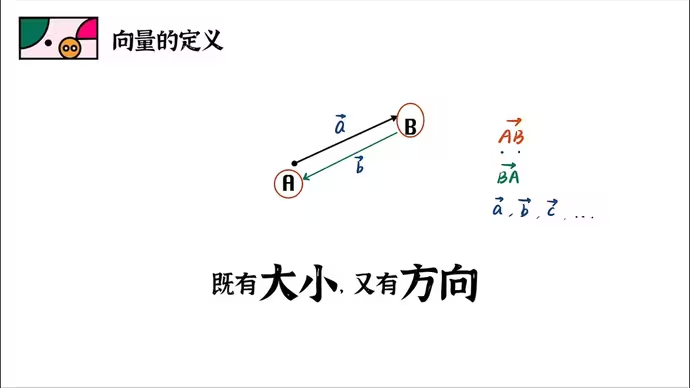
向量中的数表示了每一个维度上有方向的位移。例如，沿x轴移动3像素，沿y轴移动5像素。那么这个向量可以表达为[3,5]，方向是从原点指向点 (3, 5)

class Vector {
    public x: number;
    public y: number;

    public constructor(x: = 0, y = 0) {
        this.x = x;
        this.y = y;
    }
}

向量的模长（长度或大小）

表示方法：向量长度的绝对值，如 |a|

public get norm(): number {
    return Math.hypot(this.x, this.y);
	// return Math.sqrt(this.x * this.x + this.y * this.y);
}

当向量模长为1时，称为单位向量
当向量长度为0时，表示零向量

基础概念

1. 相等向量

若两个向量大小相等，方向也相等，即为相等向量。不需要起始终点是一样的，相等向量可以是平移和重合的

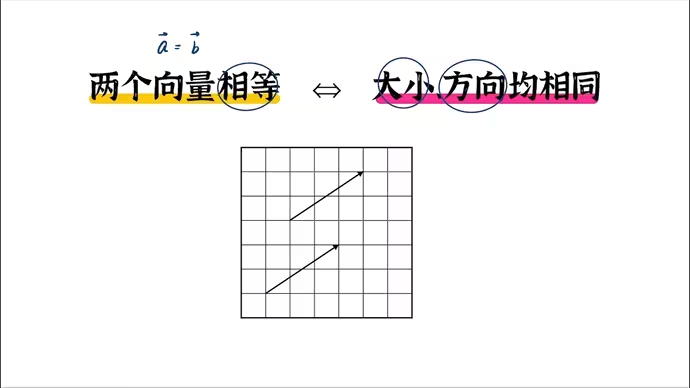
2. 平行向量

当两个向量所在直线平行时，为平行向量。向量平行有两种情况：方向相同与相反

零向量方向任意，故它与任何向量都平行

向量的数乘

数乘：向量与一个系数相乘，这个系数可以是任何数，如果是 -1，得到相反向量

- \vec{A B} = \vec{B A}

public multiply(s: number): void {
	this.x *= s;
	this.y *= s;
}

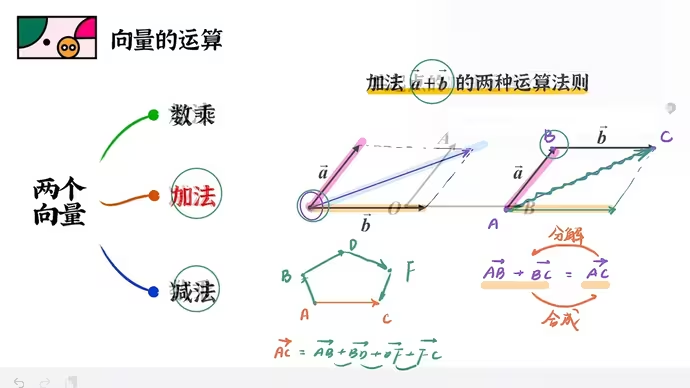
向量的加法

当两个向量起始点一样时，加法遵从平行四边形法则。当一个向量的终点是一个向量的起点时，加法遵从三角形法则（本质也是平行四边形法则）

由三角形法则，可以将一个向量拆为多个向量，但向量间要首尾相接，如图中的五边形（即运算时保证向量间上一个的终点为下一个的起点）

public static add(v1: Vector, v2: Vector): Vector {
	return new Vector(v1.x + v2.x, v1.y + v2.y);
}

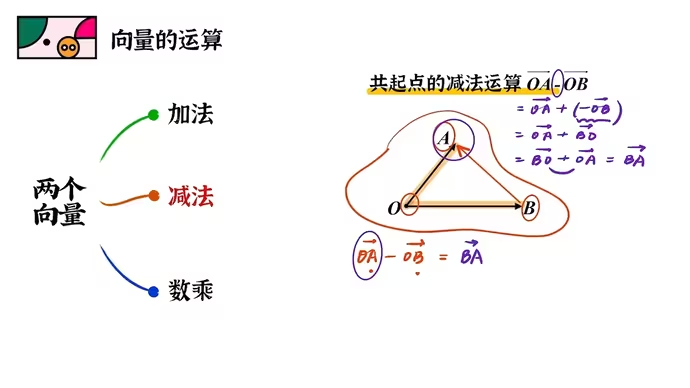
向量的减法

共起点的减法运算

\vec{O A} - \vec{O B} = \vec{O A} + \vec{B O} = \vec{B O} + \vec{O A} = \vec{B A}

public static subtract(v1: Vector, v2: Vector): Vector {
	return new Vector(v1.x - v2.x, v1.y - v2.y);
}

向量的中线

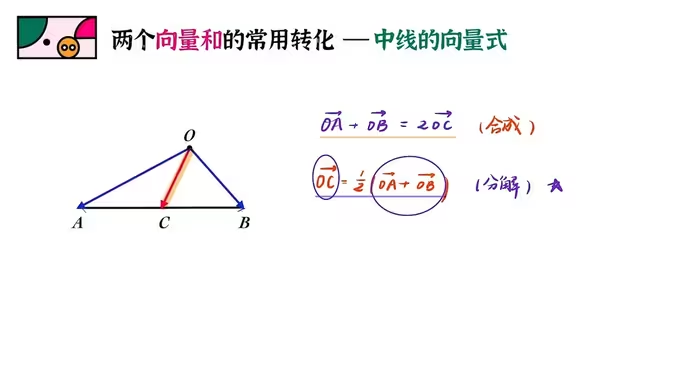
\vec{O A} + \vec{O B} = 2 \vec{O C} \vec{O C} = \frac{1}{2} (\vec{O A} + \vec{O B})

向量的归一化（标准化）

很多时候我们要在游戏中使用向量来表示一个物体的方向，而不关心其大小。这样情况下使用“单位向量”将非常方便。所谓单位向量就是大小为1的向量。将一个向量变成单位向量的操作我们称之为归一化，也叫做标准化。

public normalize(): void {
	if (this.norm === 0) {
		return;
	}
	this.multiply(1 / this.norm);
}

向量旋转

逆时针时θ为正数，顺时针时θ为负数

推导：下标 0 代表旋转前，下标 1 代表旋转后

\begin{array}{r} x 0 = | R | \times c o s α \\ y 0 = | R | \times s i n α \\ x 1 = | R | \times c o s (α + θ) \\ y 1 = | R | \times s i n (α + θ) \\ x 1 = | R | \times (c o s α c o s θ - s i n α s i n θ) \\ y 1 = | R | \times (s i n α c o s θ + c o s α s i n θ) \\ x 1 = x 0 \times c o s θ - y 0 \times s i n θ \\ y 1 = x 0 \times s i n θ + y 0 \times c o s θ \end{array}

public rotate(angle: number): void {
  const x0 = this.x, y0 = this.y
  const cos = Math.cos(angle);
  const sin = Math.sin(andle);
  this.x = x0 * cos - y0 * sin
  this.y = x0 * sin + y0 * cos
}

向量点乘

点乘的公式表示为：A·B

点乘的结果为 A 向量在 B 向量上的投影乘以 B向量

\begin{array}{r} \vec{A} \cdot \vec{B} = | A | \times c o s 𝛳 \times | B | \end{array}

满足以下定律：

\begin{array}{r} \vec{A} \cdot \vec{B} = \vec{B} \cdot \vec{A} \\ \vec{A} \cdot (\vec{B} + \vec{C}) = \vec{A} \cdot \vec{B} + \vec{A} \cdot \vec{C} \\ (k \vec{A}) \cdot \vec{B} = \vec{A} \cdot (k \vec{B}) = k (\vec{A} \cdot \vec{B}) \end{array}

点乘计算

\begin{array}{r} \vec{a} \cdot \vec{b} = (\begin{array}{c} x_{a} \\ y_{a} \\ z_{a} \end{array}) \cdot (\begin{array}{c} x_{b} \\ y_{b} \\ z_{b} \end{array}) = x_{a} x_{b} + y_{a} y_{b} + z_{a} z_{b} \end{array}

public static dotProduct(v1: Vector, v2: Vector): number {
	return v1.x * v2.x + v1.y * v2.y;
}

几何意义一：计算这两个向量的夹角

将两个向量归一化后，进行点乘，结果为 cos𝛳 （A·B = 1 * cos𝛳 * 1 = cos𝛳）

public static angle(v1: Vector, v2: Vector): number {
	let a = Vector.dotProduct(v1, v2);
	let b = v1.norm * v2.norm;
	let c = a / b;
	let rad = Math.acos(c);
	let deg = rad * 180 / Math.PI;
	return deg;
}

几何意义二：判断两个向量是否大致都在同一个方向

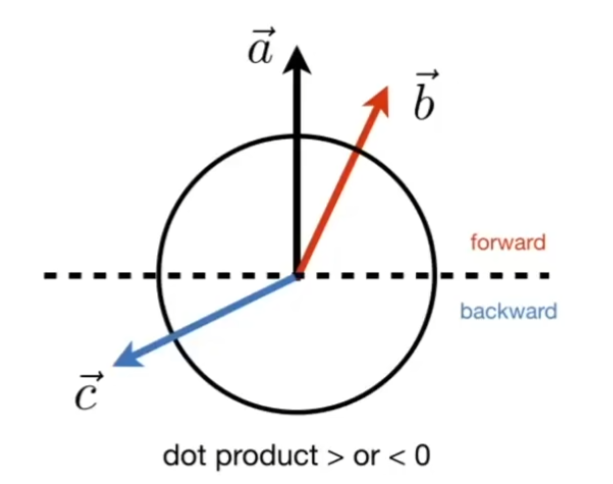
上图的 a 和 b 点乘会大于0，a 和 c 点乘会小于0，在虚线上的向量和 a 点乘会等于 0

怎么判断物体是否在人的前方还是后方
向量a：人的正前方方向向量
向量b：人指向物体的方向向量
向量a和b夹角，在0~180度的范围内的前提下：
当 a·b 大于 0，意味着 cos𝛳 大于 0，cos𝛳 大于 0 意味着夹角 𝛳 是 0-90 度，说明物体在人的前方
当 a·b 小于 0，意味着 cos𝛳 小于 0，cos𝛳 小于 0 意味着夹角 𝛳 是 90-180 度，说明物体在人的后方

几何意义三：两个向量的接近程度

A · B 越接近 1，两者越接近

A · B 为 0，两者垂直

A · B 越接近 -1，两者越远离，直到最后为 -1，则两个向量完全相反

向量叉乘

向量叉乘公式：

\begin{array}{r} c . x = a . y \times b . z - a . z \times b . y \\ c . y = a . z \times b . x - a . x \times b . z \\ c . z = a . x \times b . y - a, y \times b . x \end{array}

叉乘也满足以下公式（矩阵更容易记)

\begin{array}{r} \vec{a} \times \vec{b} = (\begin{array}{c} 0 & - z_{a} & y_{a} \\ z_{a} & 0 & - x_{a} \\ - y_{a} & x_{a} & 0 \end{array}) (\begin{array}{c} x_{b} \\ y_{b} \\ z_{b} \end{array}) \end{array}

满足以下定律：

没有交换律
有分配律和结合律

\begin{array}{r} \vec{a} \times \vec{b} = - \vec{b} \times \vec{a} \vec{a} \times \vec{a} = \vec{0} \\ \vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} + \vec{c} \\ \vec{a} \times (k \vec{b}) = k (\vec{a} \times \vec{b}) \end{array}

几何意义一：计算 Z 轴坐标

\begin{array}{r} \vec{x} \times \vec{y} = + \vec{z} \vec{y} \times \vec{x} = - \vec{z} \end{array}

几何意义二：右手螺旋定则判断方向

方向：c 向量的方向会垂直于 a 和 b 向量，垂直是向上还是向下，根据右手螺旋法则判断，如果是 a 叉乘 b，则右手从 a 向 b 握拳，拇指方位即为 c 的方向。

几何意义三：判断左和右

判断物品A在物品B的左边还是右边，计算物品A的方向向量，和AB向量，这两个向量归一化的叉乘小于零和大于零分别可能在左边或右边

几何意义四：判断内和外

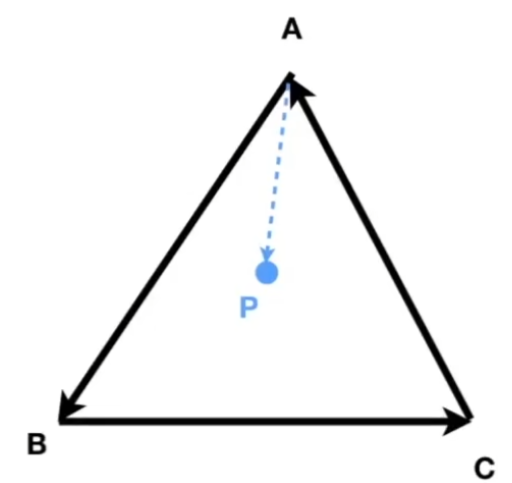
如上图， P 点在三角形 ABC 的内部，则从逆时针方向（A -> B -> C）

一定有以下三个叉乘，方向一样

\begin{array}{r} \vec{A B} \times \vec{A P} \\ \vec{B C} \times \vec{B P} \\ \vec{C A} \times \vec{C P} \end{array}

顺时针也一样，也会方向一样点在边上，则叉乘结果为 0

j几何意义四：计算三角形表面积

大小：c的模 = A的模 × B的模 × sin𝛳

计算三角形表面积，c的模 = 三角形表面积 * 2

向量类中一些方便的接口

/**
 * 复制另外一个向量的值
 */
public copy(v: Vector): void {
    this.x = v.x;
    this.y = v.y;
}

/**
 * 设置向量的值
 */
public setTo(x: number, y: number): void {
    this.x = x;
    this.y = y;
}

/**
 * 新建一个向量，Vector(1, 1)
 */
public static one(): Vector {
    return new Vector(1, 1);
}

/**
 * 新建一个向量，Vector(0, 0)
 */
public static zero(): Vector {
    return new Vector(0, 0);
}

/**
 * 新建一个向量，Vector(-1, 0)
 */
public static left(): Vector {
    return new Vector(-1, 0);
}

/**
 * 新建一个向量，Vector(1, 0)
 */
public static right(): Vector {
    return new Vector(1, 0);
}

/**
 * 新建一个向量，Vector(0, 1)
 */
public static down(): Vector {
    return new Vector(0, 1);
}

/**
 * 新建一个向量，Vector(0, -1)
 */
public static up(): Vector {
    return new Vector(0, -1);
}