动态规划2--基础题

最大子序和（53）

题目

  • 状态：dp[i] 表示以 nums[i] 结尾 的 连续 子数组的最大和
  • 方程
dp[i]={dp[i−1]+nums[i],if dp[i−1] > 0nums[i],if dp[i−1] ≤ 0

因为求最大值，所以可以直接取最大值

dp[i]=max{nums[i],dp[i−1]+nums[i]}
public int maxSubArray(int[] nums) {
	int len = nums.length;
	int[] dp = new int[len];
	dp[0] = nums[0];
	int res = nums[0];
	
	for (int i = 1; i < len; i++) {
		dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);
		res = Math.max(res, dp[i]);
	}
	
	return res;
}

观察到只与 dp[i] 只与 dp[i - 1] 有关，顾可降维，优化空间复杂度

public int maxSubArray(int[] nums) {
	int dp = nums[0], res = nums[0];
	
	for (int i = 1; i < nums.length; i++) {
		dp = Math.max(nums[i], dp + nums[i]);
		res = Math.max(res, dp);
	}
	
	return res;
}

不同路径（62）

题目

  • 状态：dp[y][x] 表示走到坐标 (y, x) 的路径总数
  • 方程：走到坐标 (y, x) 可以从上方下来，也可以从左边过来，路径总数是二者之和
dp[y][x]=dp[y][x−1]+dp[y−1][x]
public int uniquePaths(int m, int n) {
    int[][] dp = new int[m][n];
    for (int y = 0; y < m; y++) dp[y][0] = 1;
    for (int x = 0; x < n; x++) dp[0][x] = 1;
    for (int y = 1; y < m; y++) {
        for (int x = 1; x < n; x++) {
            dp[y][x] = dp[y][x - 1] + dp[y - 1][x];
        }
    }
    return dp[m - 1][n - 1];
}

观察到左边第一行和上边第一行，肯定都为 1，因为 dp[y, x] 肯定与 dp[y - 1, x] 有关，可以用一维数组记录一行每列的dp 值，新一行继承上一行的值，再加上从左边过来的

public int uniquePaths(int m, int n) {
    int[] dp = new int[n];
    dp[0] = 1;
    for (int y = 0; y < m; y++) {
        for (int x = 1; x < n; x++) {
            dp[x] += dp[x - 1];
        }
    }
    return dp[n - 1];
}

不同路径 II（63）

题目

  • 状态：dp[y][x] 表示走到坐标 (y, x) 的路径总数
  • 方程
dp[y][x]={dp[y−1][x−1],(y,x) 无障碍物0,(y,x) 有障碍物
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
    int m = obstacleGrid.length, n = obstacleGrid[0].length;
    int dp[][] = new int[m][n];
    for (int y = 0; y < m && obstacleGrid[y][0] == 0; y++) dp[y][0] = 1;
    for (int x = 0; x < n && obstacleGrid[0][x] == 0; x++) dp[0][x] = 1;
    for (int y = 1; y < m; y++) {
        for (int x = 1; x < n; x++) {
            if (obstacleGrid[y][x] == 0) {
                dp[y][x] = dp[y - 1][x] + dp[y][x - 1];
            }
        }
    }
    return dp[m - 1][n - 1];
}

降维，优化空间复杂度。dp[x] += dp[x - 1] 即从左边过来的，y++ 即从上边过来的

public int uniquePathsWithObstacles(int[][] obstacleGrid) {
    int m = obstacleGrid.length, n = obstacleGrid[0].length;
    int dp[] = new int[n];
    dp[0] = obstacleGrid[0][0] == 1 ? 0 : 1;
    for (int y = 0; y < m; y++) {
        for (int x = 0; x < n; x++) {
            if (obstacleGrid[y][x] == 1) { // 有障碍物，则不可能从上面或左边过来了
                dp[x] = 0; // 清除上一行缓存，即不可能从上面过来
                continue;  // 不走下面判断，即不可能从左边过来
            }
            if (x > 0) dp[x] += dp[x - 1];
        }
    }
    return dp[n - 1];
}

最小路径和（64）

题目

  • 状态：dp[y][x] 表示走到坐标 (y, x) 的最小路径和
  • 方程
dp[y][x]=max{dp[y−1][x],d[y][x−1]}+grid[y][x]
public int minPathSum(int[][] grid) {
    int m = grid.length, n = grid[0].length;
    int[][] dp = new int[m][n];
    dp[0][0] = grid[0][0];
    for (int y = 1; y < m; y++) dp[y][0] = dp[y - 1][0] + grid[y][0];
    for (int x = 1; x < n; x++) dp[0][x] = dp[0][x - 1] + grid[0][x];
    for (int y = 1; y < m; y++) {
        for (int x = 1; x < n; x++) {
            dp[y][x] = Math.min(dp[y - 1][x], dp[y][x - 1]) + grid[y][x];
        }
    }
    return dp[m - 1][n - 1];
}

这里降维需要多增加判断，即增加时间复杂度，所以就不降纬了

爬楼梯（70）

题目

  • 状态：dp[i] 表示爬到第 i 阶楼梯的方法数
  • 方程
dp[i]=dp[i−1]+dp[i−2]
public int climbStairs(int n) {
    int[] dp = new int[n + 1];
    dp[0] = dp[1] = 1;
    for (int i = 2; i < n + 1; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}

降维，优化空间复杂度。

public int climbStairs(int n) {
    int a = 0, b = 1, c = 1;
    for (int i = 2; i < n + 1; i++) {
        a = b;
        b = c;
        c = a + b;
    }
    return c;
}

解码方法（91）

题目

  • 状态：dp[i] 表示到字符串第 i 位置时有多少种解码方法
  • 方程
dp[i]={dp[i−1],1 ≤ a ≤ 9dp[i−2],10 ≤ b ≤ 26dp[i−1]+dp[i−2],1 ≤ a ≤ 9, 10 ≤ b ≤ 26
public int numDecodings(String s) {
    char[] cs = s.toCharArray();
    if (cs[0] == '0') return 0;
    int len = cs.length;

    int[] dp = new int[len + 1];
    dp[0] = dp[1] = 1;
    for (int i = 1; i < len; i++) {
        int a = cs[i] - '0', b = (cs[i - 1] - '0') * 10 + a;
        if (a >= 1 && a <= 9) dp[i + 1] = dp[i];
        if (b >= 10 && b <= 26) dp[i + 1] += dp[i - 1];
    }
    return dp[len];
}

不同的二叉搜索树（96）

题目

  • 状态：dp[i] 代表有 i 个节点时，一共有多少种二叉搜索树
  • 当有 n 个节点时，以 m 作为根节点，一共有 f(m - 1) * f(n - m) 种二叉搜索树，则 dp[i] = f(1) + ... + f(i)
  • 而算 dp[i] 时，会依赖 dp[0] 到 dp[i - 1] 的结果（缓存下来，不用重复计算）

 public int numTrees(int n) {
    int[] dp = new int[n + 1];
    dp[0] = dp[1] = 1; // dp[0] 为 1，保证子树节点个数为 0 时，也能正常计算

    for (int i = 2; i < n + 1; i++) { // i 表示现在一共有多少个节点
        for (int j = 1; j <= i; j++) { // j 表示现在的根节点
            dp[i] += dp[j - 1] * dp[i - j];
        }
    }

    return dp[n];
}

三角形最小路径和（120）

题目

  • 状态：dp[y][x] 代表三角形中 (y, x) 位置的最小路径和
  • 方程
dp[y][x]=min{dp[y+1][x],dp[y+1][x+1]}+t[y][x]
public int minimumTotal(List<List<Integer>> triangle) {
    int n = triangle.size();
    int[][] dp = new int[n + 1][n + 1]; // 防止越界

    for (int y = n - 1; y >= 0; y--) { // 自底向上，从最后一行开始
        for (int x = 0; x <= y; x++) {
            dp[y][x] = Math.min(dp[y + 1][x], dp[y + 1][x + 1]) + triangle.get(y).get(x);
        }
    }

    return dp[0][0];
}

降维，减少空间复杂度。这一行只跟下一行有关，而且下一行的结果都保存在 dp 里

public int minimumTotal(List<List<Integer>> triangle) {
    int n = triangle.size();
    int[] dp = new int[n + 1]; // 防止越界

    for (int y = n - 1; y >= 0; y--) { // 自底向上，从最后一行开始
        for (int x = 0; x <= y; x++) {
            dp[x] = Math.min(dp[x], dp[x + 1]) + triangle.get(y).get(x);
        }
    }

    return dp[0];
}

单词拆分（139）

题目

  • 状态：dp[i]表示前 i 个字符是否可以在字典中找到
public boolean wordBreak(String s, List<String> wordDict) {
    int n = s.length();
    Set set = new HashSet(wordDict);
    boolean[] dp = new boolean[n + 1];
    dp[0] = true; // 空字符串

    for (int r = 1; r <= n; r++) { // 字串的右边界（不包括）
        for (int l = 0; l <= r - 1; l++) { // 字串的左边界
            // dp[1] 表示第一个字符是否可以在字典中找到
            // substring(1, r) 表示从第二个字符开始截取
            if (dp[l] && set.contains(s.substring(l, r))) {
                dp[r] = true;
                break;
            }
        }
    }

    return dp[n];
}

乘积最大子数组（152）

题目

  • 状态
    • maxDp[i] 表示以 i 结尾的子数组的最大乘积
    • minDp[i] 表示以 i 结尾的子数组的最小乘积
  • 方程：由于存在负数，那么会导致最大的变最小的，最小的变最大的
maxDp[i]=max{nums[i],maxDp[i−1]×nums[i],minDp[i−1]×nums[i]}minDp[i]=min{nums[i],maxDp[i−1]×nums[i],minDp[i−1]×nums[i]}
public int maxProduct(int[] nums) {
    int n = nums.length, max = nums[0];
    int[] maxDp = new int[n];
    int[] minDp = new int[n];
    maxDp[0] = nums[0]; minDp[0] = nums[0];

    for (int i = 1; i < n; i++) {
        maxDp[i] = Math.max(nums[i], Math.max(maxDp[i - 1] * nums[i], minDp[i - 1] * nums[i]));
        minDp[i] = Math.min(nums[i], Math.min(maxDp[i - 1] * nums[i], minDp[i - 1] * nums[i]));
        max = Math.max(max, maxDp[i]);
    }
    return max;
}

打家劫舍（198）

题目

  • 状态：dp[i] 代表前 i 个房子在满足条件下的能偷窃到的最高金额
  • 方程：不抢第 i 家，即为 dp[i - 1]；抢第 i 家，即为 dp[i - 2] + nums[i]
dp[i]=max{dp[i−1],dp[i−2]+nums[i]}
public int rob(int[] nums) {
    int n = nums.length;
    int[] dp = new int[n + 1];
    dp[0] = 0; dp[1] = nums[0];

    for (int i = 2; i < n + 1; i++) {
        dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i - 1]);
    }
    return dp[n];
}

空间优化，dp[i] 只和 dp[i - 1] 及 dp[i - 2] 有关，所以完全可以用两个变量完成

public int rob(int[] nums) {
     int a = 0, b = 0; // a: -2 家，b：-1 家
     for (int num : nums) { // num：第 i 家（i 从 0 开始）
         int dp = Math.max(b, a + num);
         a = b;
         b = dp;
     }
     return b;
 }

最大正方形（221）

题目

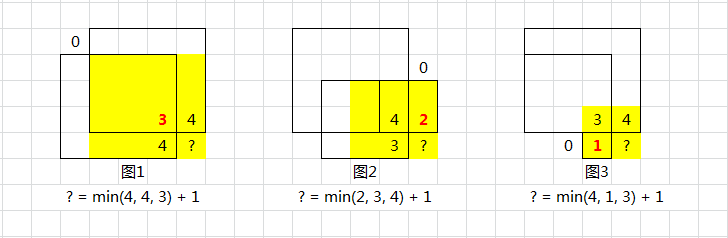
  • 状态：dp[y][x] 是以 matrix(y - 1, x - 1) 为 右下角 的正方形的最大边长
  • 方程：格子为 1 ，若要形成的正方形，则需要左上、左、上均为 1，想要形成更大的正方形，根据木桶短板原理，取最小一个
dp[y][x]=min{dp[y−1][x−1],dp[y][x−1],dp[y−1][x]}+1

public int maximalSquare(char[][] matrix) {
    int n = matrix.length, m = matrix[0].length, max = 0;
    int[][] dp = new int[n + 1][m + 1];

    for (int y = 0; y < n; y++) {
        for (int x = 0; x < m; x++) {
            if (matrix[y][x] == '1') {
                dp[y + 1][x + 1] = Math.min(dp[y][x], Math.min(dp[y][x + 1], dp[y + 1][x])) + 1;
                max = Math.max(max, dp[y + 1][x + 1]);
            }
        }
    }
    return max * max;
}

完全平方数（279）

题目

  • 状态：dp[i] 表示i的完全平方和的最少数量
  • 方程：dp[i] = min(dp[i], dp[i - j * j] + dp[j * j])，但 dp[j * j] 必定为 1，所以有以下简写
dp[i]=min{dp[i],dp[i−j∗j]+1}
public int numSquares(int n) {
    int[] dp = new int[n + 1];
    for (int i = 1; i <= n; i++) {
        dp[i] = i; // 最差情况，1 + 1 + 1 = 3
        for (int j = 1; i - j * j >= 0; j++) { // 找一个完全平方数（j * j）
            dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
        }
    }
    return dp[n];
}

最长递增子序列（300）

题目

  • dp[i] 代表 nums 以 nums[i] 结尾的最长子序列长度
  • 方程
    • 以第 i 个数字为结尾，即要求 nums[i] 必须被选取，则初始长度至少为 1
    • 如果当前的数 nums[i] 大于之前的某个数，那么 nums[i] 就可以接在这个数后面形成一个更长的 LIS 。把前面的 i 个数都看了， LIS[i] 就是它们的最大值加 1。即比当前数要小的那些里头，找最大的，然后加 1。
dp[i]=max{dp[i],dp[j]+1}if  j < i  &  nums[i] > nums[j] 
public int lengthOfLIS(int[] nums) {
    int n = nums.length, max = 1;
    int[] dp = new int[n];
    Arrays.fill(dp, 1); // 自己本身就是一个子序列

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < i; j++) {
            if (nums[i] > nums[j]) {
                dp[i] = Math.max(dp[i], dp[j] + 1);
            }
        }
        max = Math.max(max, dp[i]);
    }

    return max;
}

整数拆分（343）

题目

  • 状态：dp[i] 表示数字 i 能够被拆分的最大乘积
  • 方程：将 i 挨个可能拆了，找到最大值
dp[i]=max{dp[i],j∗(i−j),j∗dp[i−j]}
public int integerBreak(int n) {
    int[] dp = new int[n + 1];
    dp[1] = 1;

    for (int i = 2; i <= n; i++) {
        for (int j = 1; j < i; j++) {
            dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
        }
    }

    return dp[n];
}

dp[1] = 1 当 i = 2，j = 1 时用到了 dp[i]，所以需要初始化

Math.max(j * (i - j), j * dp[i - j]) 存在情况，j * (i - j) 大于 j * dp[i - j]

  • 如 2 = 1 + 1，dp[2] = 1*1 = 1，而当 3 拆成 1+2 时，dp[3] 是等于 1*2 的，而不是 1*dp[2]

摆动序列（376）

题目

  • 状态
    • up[i] 表示 nums[0:i] 中最后两个数字递增的最长摆动序列长度
    • down[i] 表示 nums[0:i] 中最后两个数字递减的最长摆动序列长度
  • 方程：情况为上升时，则 up 在 down 上加一，为下降时，则 down 在 up 上加一，其他时候往上继承
up[i]={down[i−1]+1,nums[i - 1] < nums[i]up[i],nums[i - 1] ≥ nums[i]down[i]={down[i−1],nums[i - 1] ≤ nums[i]up[i−1]+,nums[i - 1] < nums[i]
public int wiggleMaxLength(int[] nums) {
    int n = nums.length;
    int[] up = new int[n], down = new int[n];
    up[0] = 1; down[0] = 1; // 虽然一个数不形成摆动序列，但数量为一。当形成摆动序列时，这个数也想算上的

    for (int i = 1; i < n; i++) {
        up[i] = up[i - 1];
        down[i] = down[i - 1];
        if (nums[i - 1] < nums[i]) { // 上升，则在下降序列基础上加一
            up[i] = down[i - 1] + 1;
        } else if (nums[i - 1] > nums[i]) { // 下降，则在上升序列基础上加一
            down[i] = up[i - 1] + 1;
        }
    }

    return Math.max(up[n - 1], down[n - 1]);
}

可观察到只与前一个变量有关，故可降维，降低空间复杂度

public int wiggleMaxLength(int[] nums) {
   int up = 1, down = 1;
   for (int i = 1; i < nums.length; i++) {
       if (nums[i - 1] < nums[i]) {
           up = down + 1;
       } else if (nums[i - 1] > nums[i]) {
           down = up + 1;
       }
   }

   return Math.max(up, down);
}

组合总和 Ⅳ（377）

题目

  • 状态：dp[i] 表示凑成总和为 i 的组合总和
  • 方程
dp[i]=∑j=0n−1∫dp[i−nums[j]]ifi≥nums[j]

以 nums = [1, 2, 3] ， target = 4 为例

  • dp[0] = 1
  • dp[1] = dp[0]（选择1）= 1
  • dp[2] = dp[0]（选择2）+ dp[1]（选择1）= 2
  • dp[3] = dp[0]（选择3）+ dp[1]（选择2）+ dp[2]（选择1）= 4
  • dp[4] = dp[1]（选择3）+ dp[2]（选择2）+ dp[3]（选择1）= 7
public int combinationSum4(int[] nums, int target) {
    int[] dp = new int[target + 1];
    dp[0] = 1; // 没有放任何物体进背包也算一种

    for (int i = 1; i <= target; i++) { // 确定背包容量
        for (int num : nums) { // 尝试所有可能
            if (i - num >= 0) dp[i] += dp[i - num];
        }
    }

    return dp[target];
}

等差数列划分（413）

题目

  • 状态：dp[i] 表示以 nums[i] 结尾的、且长度大于等于 3 的连续等差数列的个数
    • 必需以 nums[i] 结尾，nums[i] 必需被选取
    • 长度大于等于 3
    • 记录的是个数，就是题目要我们找的长度大于等于 3 的连续子数组（且是等差数列）的个数
  • 方程：如果 nums[i] 能够接在 nums[i - 1] 之后形成一个长度更长的（在原数组上连续的）等差数列，那么 dp[i] = dp[i - 1] + 1
dp[i]=dp[i−1]+1ifnums[i]−nums[i−1]==nums[i−1]−nums[i−2]
public int numberOfArithmeticSlices(int[] nums) {
    int n = nums.length, res = 0;
    int[] dp = new int[n];

    for (int i = 2; i < n; i++) {
        if (nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2]) {
            dp[i] = dp[i - 1] + 1;
            res += dp[i];
        }
    }

    return res;
}

斐波拉契数列（509）

题目

  • 状态：dp[i] 表示第 i 个斐波拉契数值
  • 方程
dp[i]=dp[i−1]+dp[i−2]
public int fib(int n) {
    if (n < 2) return n;
    int[] dp = new int[n + 1];
    dp[1] = 1;

    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }

    return dp[n];
}

使用最小花费爬楼梯（746）

题目

  • 状态：dp[i] 代表登上第 i 级台阶的最小花费
  • 方程
    • 先踏上第i-2级台阶（最小总花费dp[i-2]），再直接迈两步踏上第i级台阶（花费cost[i]），最小总花费dp[i-2] + cost[i]
    • 先踏上第i-1级台阶（最小总花费dp[i-1]），再迈一步踏上第i级台阶（花费cost[i]），最小总花费dp[i-1] + cost[i]
dp[i]=min(dp[i−2],dp[i−1])+cost[i]
public int minCostClimbingStairs(int[] cost) {
    int n = cost.length;
    int[] dp = new int[n];
    dp[0] = cost[0]; dp[1] = cost[1]; // 初始时的最小花费

    for (int i = 2; i < n; i++) {
        dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
    }

    return Math.min(dp[n - 2], dp[n - 1]); // 寻找从后两层最小的花费
}

环形子数组的最大和（918）

题目

  • 前提：需要掌握 **53.最大子序和 ** 空间优化后的解法

最大和有两种情况：

  1. 最大子序和就在数组中
  2. 最大自序和的子数组一部分在首，一部分在尾，则可以转换为第一种

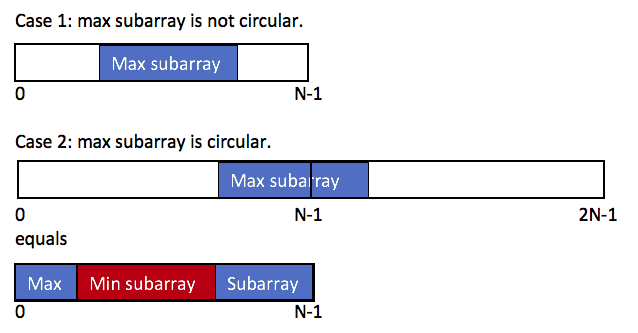
即 res = max(最大子数组和，数组总和-最小子数组和)

证明第二种情况

max(前缀数组+后缀数组)=max(数组总和−子数组)=数组总和+max(−子数组)=数组总和−min(子数组)

注意极端情况，数组全部为负值，则第一种情况，结果为最大的负数，第二种情况，结果为 0，如果直接返回二者的最大值，则肯定为 0，但示例 5 告诉我们，这种极端情况要返回最大的负数，所以需要特判一下

total为数组的总和，max为最大子数组和，min为最小子数组和，maxdp为以当前值结尾的最大子数组和，mindp为当前值结尾的最小子数组和

public int maxSubarraySumCircular(int[] nums) {
    // 考虑到存在全为负值，max 和 min 初始不能为 0
    int total = 0, max = nums[0], maxdp = 0, min = nums[0], mindp = 0;

    for (int num : nums) {
        maxdp = Math.max(maxdp + num, num);
        max = Math.max(max, maxdp);
        mindp = Math.min(mindp + num, num);
        min = Math.min(min, mindp);
        total += num;
    }

    return max > 0 ? Math.max(max, total - min) : max;
}

最低票价（983）

题目

  • 状态：dp[i] 表示到下标为 i 的这一天，旅行所需要的最低消费
  • 方程：
dp[i]={dp[i−1],i 不在 days 中min{dp[i−1]+costs[0],dp[i−7]+costs[1],dp[i−30]+costs[2]},i 在 days 中
public int mincostTickets(int[] days, int[] costs) {
    int lastDay = days[days.length - 1];
    int[] dp = new int[lastDay + 1];
    int index = 0; // 检测 i 是不是在 days 中

    for (int i = 1; i <= lastDay; i++) {
        if (i == days[index]) {
            // 比较三个的最小值
            int cost = Integer.MAX_VALUE;
            cost = Math.min(cost, dp[i - 1] + costs[0]);
            cost = Math.min(cost, dp[Math.max(i - 7, 0)] + costs[1]);
            cost = Math.min(cost, dp[Math.max(i - 30, 0)] + costs[2]);
            dp[i] = cost;

            index++; // 寻找下一个 i
        } else {
            dp[i] = dp[i - 1];
        }
    }
    return dp[lastDay];
}
最近更新：:
Contributors: kingmusi