斜率K

实践1

画一条与已知线（可能为斜线）垂直的长度为40的线

求出已知斜线的斜率，k = (y2 - y1) / (x2 - x1)
求出垂直线的斜率，k1 = -1 / k
垂直线的一个端点就是已知斜线某一个端点，(x1, y1)，另一个点要求的为(x, y)，如下图

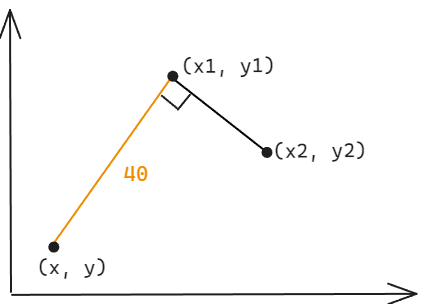
根据斜率公式，y = k1 * (x - x1) + y1，所以需要求出 x 即可知道 y
如下图，x = x1 - b

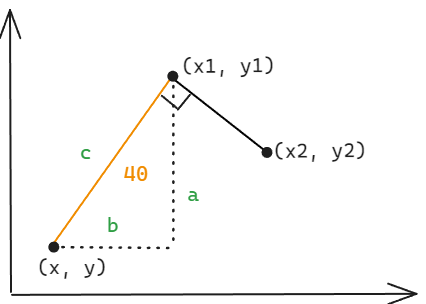
根据勾股定理a^2 + b^2 = c^2和斜率k1 = a / b公式，可得 k1^2 * b^2 + b^2 = c^2
上面公式简化得

b = \sqrt{\frac{c^{2}}{1 + k 1^{2}}}

所以可得到点 (x, y)

(x 1 - \sqrt{\frac{c^{2}}{1 + k 1^{2}}}, k 1 \times (x - x 1) + y 1)

type Point = [number, number]
function drawVerticalLine(ctx: CanvasRenderingContext2D, p1: Point, p2: Point, length = 40) {
  const k = (p1[1] - p2[1]) / (p1[0] - p2[0]) // 已知线斜率
  const k1 = -1 / k // 垂直线斜率
  
  // 代码上实现有个问题，如果已知线平行于 x 轴，则 k 为 0，k1 为无限大，所以需要特殊处理
  const isVerticalX = k === 0 // 是否垂直于x轴
  const x = isVerticalX ? p1[0] : p1[0] - Math.sqrt(length * length / (1 + Math.pow(k1, 2)))
  const y = isVerticalX ? p1[1] + length : k1 * (x - p1[0]) + p1[1]
  
  ctx.beginPath()
  ctx.strokeStyle = 'black'
  // 绘制线
  ctx.moveTo(x, y)
  ctx.lineTo(...p1)
  ctx.stroke()
  ctx.closePath()
}

斜率K

相关公式

实践1